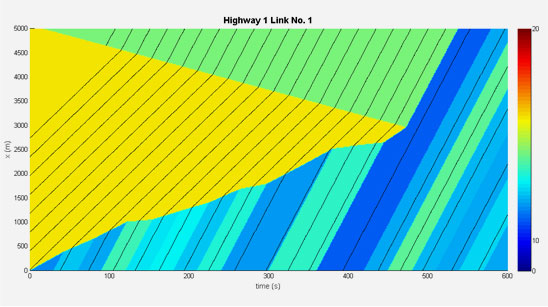
The computation of solutions to the LWR model on networks is of critical importance. Forward simulations are widely used for forecast, estimation and control problems, and are the basis of some estimation (Kalman Filter and its derivatives) and control (Model Predictive Control) algorithms.
Recently, Lax-Hopf methods have been derived to compute the solution to the LWR model on single roads. Their extension to network is straightforward. However, Lax-Hopf methods are not faster than classical methods based on the discretization of the PDE, for example the Cell Transmission Model (Godunov discretisation of the LWR model). In this work, we focus on the specific problem of computing solutions to the LWR model with triangular Hamiltonians over networks. We demonstrate that solutions can be computed at the boundaries with significantly less operations than required by Lax-Hopf methods, while maintaining exactness. The resulting algorithm allows the forward computation of boundary demand and supplies, which can be fed into junction models to determine the actual boundary conditions over all links. This algorithm is in practice nearly as fast as the Link Transmission Model, yet allows the integration of initial conditions.